ในปัจจุบันมีการนำโมเดล machine learning รูปแบบต่าง ๆ มาใช้งานอย่างกว้างขวาง เช่น ใช้ในการจำแนกอีเมลขยะออกจากอีเมลจริง, ใช้ในการแนะนำวิดิโอต่าง ๆ ที่ผู้ใช้อาจจะสนใจ, ใช้ในการปรับแต่งภาพถ่ายในโทรศัพท์ หรือ การทำงานของประสาทเทียม (Neural Network) โดยหนึ่งในโมเดลที่ได้รับความนิยมมากที่สุด คือ เครือข่ายประสาทเทียม (Artificial Neural Networks – ANNs) ในบทความนี้ เราจะพาไปเจาะลึกถึงโครงสร้างและหลักการทำงาน รวมไปถึงประวัติของโมเดลเครือข่ายประสาทเทียมกันนะครับ
ประวัติของโมเดลเครือข่ายประสาทเทียม
แนวคิดเรื่องเครือข่ายประสาทเทียม เริ่มจากโมเดล Perceptron ที่ McCulloch and Pitts ได้เสนอขึ้นมาในปี 1943 และมีการสร้างเครื่อง Perceptron ขึ้นมาทดลองใช้จริงในปี 1958 โดยโมเดลนี้ ใช้สมการการตัดสินใจ (decision function) ดังต่อไปนี้
[latexpage]
\begin{equation}
f(\mathbf{x}) =
\begin{cases}
1, & \text{if } \mathbf{w} \cdot \mathbf{x} + b > 0\\
0, & \text{otherwise}
\end{cases}
\end{equation}
โดยที่ $\mathbf{w}$ เป็นเวกเตอร์น้ำหนัก และ $b$ เป็นค่าไบแอสที่โมเดลจะเรียนรู้ขึ้นมาระหว่างการฝึกฝน
อัลกอริทึมในการฝึกฝนโมเดล Perceptron มีดังต่อไปนี้
- สุ่มค่าเริ่มต้นของ $\mathbf{w}$ และ $b$
- เลือกค่า learning rate $r$ ระหว่าง 0 และ 1
- สำหรับจุดข้อมูล $(\mathbf{x}, y)$ คำนวณค่า $f(\mathbf{x}) = \mathbf{w}\cdot\mathbf{x} + b$
- ปรับค่า $\mathbf{w}$ และ $b$ โดยใช้สมการ $\mathbf{w} = \mathbf{w} + r(y – f(\mathbf{x}))\mathbf{x}$ และ $b = b + r(y – f(\mathbf{x}))$
- ทำซ้ำตามจำนวนครั้งที่ต้องการหรือจนกว่าอัตราความผิดพลาดจะน้อยกว่าที่กำหนด
หรือหากอธิบายด้วยภาษาพูด วิธีการฝึกฝนก็คือ เมื่อโมเดลทำนายผิดจาก 1 เป็น 0 ให้บวกจุดข้อมูลที่ผิดพลาดคูณกับ $r$ นั้นเข้าไปใน $\mathbf{w}$ แต่หากทำนายผิดจาก 0 เป็น 1 ให้ลบจุดข้อมูลคูณกับ $r$ ออกจาก $\mathbf{w}$
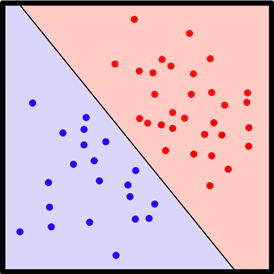
โมเดลนี้ มีข้อจำกัดคือ สมการการตัดสินใจเป็นสมการเชิงเส้น ทำให้ขาดความยืดหยุ่น เนื่องจากบางชุดข้อมูลอาจจะไม่สามารถแยกแยะ หรือทำนายได้ด้วยสมการเชิงเส้น อาจจะต้องการสมการการตัดสินใจที่มีความซับซ้อนมากขึ้น
ในปี 1969 Marvin Minsky ได้เสนอตัวอย่างหนึ่งที่ชัดเจนที่สุดคือ Perceptron ไม่สามารถทำนายค่าของข้อมูลที่มีความสัมพันธ์กันแบบ XOR ได้ กล่าวคือ หากเรามีจุดข้อมูล $(x_1, x_2, y)$ โดยที่ $y = x_1 \oplus x_2$ และพยายามใช้ฟังก์ชันของ Perceptron ในการเลียนแบบความสัมพันธ์นี้โดยการแก้สมการหาค่า $\mathbf{w}$ และ $b$ ที่ทำให้
\begin{equation}
y = x_1 \oplus x_2 = f(\mathbf{x}) =
\begin{cases}
1, & \text{if } \mathbf{w} \cdot \mathbf{x} + b = w_1x_1 + w_2x_2 + b > 0\\
0, & \text{otherwise}
\end{cases}
\end{equation}
จะพบว่าไม่มีค่า $w_1, w_2$ และ $b$ ที่เป็นคำตอบของสมการนี้
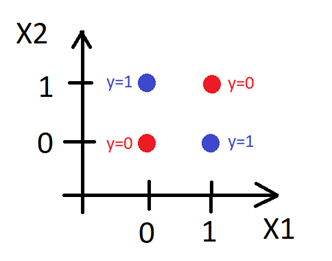
การแก้ปัญหา XOR นี้มีหลายวิธี วิธีที่ง่ายที่สุดคือการดัดแปลงเวกเตอร์ $\mathbf{x} = (x_1, x_2)$ โดยการเพิ่ม $x_3 = x_1\cdot x_2$ เข้าไปในเวกเตอร์ $\mathbf{x}$ ทำให้ $\mathbf{x} = (x_1, x_2, x_1 \cdot x_2)$ เมื่อเพิ่มขนาดเวกเตอร์ $\mathbf{x}$ แล้ว ฟังก์ชั่น $f(\mathbf{x})$ จึงต้องเพิ่มขนาดเวกเตอร์น้ำหนัก $\mathbf{w}$ โดยมี $w_3$ เพิ่มเข้าไปด้วย ทำให้สมการการตัดสินใจใหม่กลายเป็น
\begin{equation}
y = x_1 \oplus x_2 = f(\mathbf{x}) =
\begin{cases}
1, & \text{if } \mathbf{w} \cdot \mathbf{x} + b = w_1x_1 + w_2x_2 +w_3x_1x_2 + b > 0\\
0, & \text{otherwise}
\end{cases}
\end{equation}
จะพบว่า $w_1 = 2, w_2 = 2, w_3 = -4, b = -1$ เป็นคำตอบหนึ่งของสมการนี้ดังจะเห็นได้จากตารางที่ 1
| $x_1$ | 0 | 0 | 1 | 1 |
| $x_2$ | 0 | 1 | 0 | 1 |
| $x_3=x_1 \cdot x_2$ | 0 | 0 | 0 | 1 |
| $y = x_1 \oplus x_2$ | 0 | 1 | 1 | 0 |
| $\mathbf{w}\cdot\mathbf{x} + b = 2x_1 + 2x_2 – 4x_3 – 1$ | -1 | 1 | 1 | -1 |
| $f(\mathbf{x})$ | 0 | 1 | 1 | 0 |
วิธีการดัดแปลงเวกเตอร์ $\mathbf{x}$ ให้สามารถใช้งานกับโมเดลที่เรามีอยู่แล้วนี้เรียกว่าวิธี feature engineering ซึ่งเป็นหัวข้อที่มีความซับซ้อน เราจะยังไม่กล่าวถึงในบทความนี้
อีกวิธีในการแก้ปัญหานี้คือ การเพิ่มขีดความสามารถให้โมเดลมีความยืดหยุ่นมากขึ้น โดยการพัฒนาขั้นต่อมานั้น เป็นการเพิ่ม layer ของ Perceptron เข้าไป โดยมีฟังก์ชันที่ไม่เป็นเชิงเส้นคั่นระหว่าง layers ดังนั้น ฟังก์ชันของแต่ละ layer คือ
\begin{equation}
f(\mathbf{x}) = \sigma (\mathbf{w}\cdot\mathbf{x} + b)
\end{equation}
โดยที่ $\mathbf{w}$ และ $b$ เป็นค่าน้ำหนักและไบแอสตามโมเดล Perceptron เดิม แต่เพิ่ม $\sigma$ เป็นฟังก์ชันที่ไม่เป็นเชิงเส้น เช่น ฟังก์ชันsigmoid, tanh หรือ ReLU เมื่อ layer หนึ่งคำนวณค่า $f(\mathbf{x})$ ได้แล้ว ก็จะส่งต่อค่า $f(\mathbf{x})$ เข้าสู่ layer ถัดไปให้คำนวณค่า $f(\mathbf{x})$ ของ layer ถัดไปเรื่อย ๆ จนเมื่อผ่าน layer สุดท้ายแล้วจึงทำนายค่าว่าเป็นเลข 0 หรือ 1 ขึ้นกับค่า $f(\mathbf{x})$ ของ layer สุดท้ายที่ได้รับมา โดยโมเดลใหม่นี้มีชื่อว่า Multi-layer Perceptron และมีการนิยามคอนเซ็ปต์ neuron ขึ้นมา เพื่อให้ง่ายต่อการวาดภาพโมเดลที่มีหลาย layer โดยนิยามให้ neuron เป็นส่วนของ layer ที่ทำหน้าที่จัดเก็บเวกเตอร์น้ำหนักและไบแอส $\mathbf{w}$ และ $b$ ของ layer นั้น ๆ และทำการคำนวณตามสมการที่ใช้ในโมเดล เช่น layer หนึ่งมีจำนวน $\mathbf{w}$ ทั้งหมด 10 ค่า ก็จะมี neuron ทั้งหมด 10 เซลล์ทำหน้าที่เก็บค่า $\mathbf{w}$ เหล่านี้
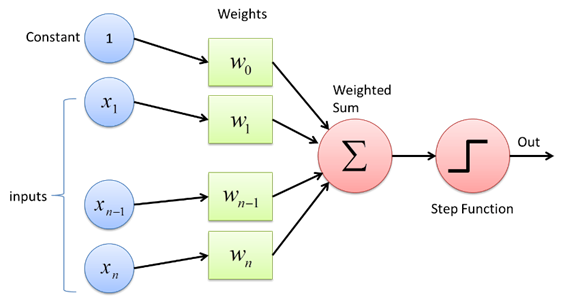
โครงสร้างพื้นฐานของโมเดล Multi-layer Perceptron ประกอบไปด้วย 3 ส่วน ได้แก่ input layer, hidden layer และ output layer โดยสามารถมี hidden layer ได้หลาย layer ตามความต้องการของผู้ออกแบบโมเดล
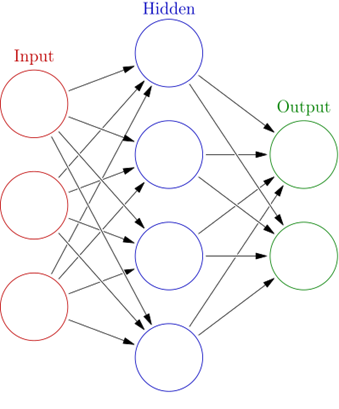
โมเดลนี้เองก็มีข้อจำกัดหลายอย่าง ทำให้นักวิจัยได้เริ่มทดลองนำ layer มาเชื่อมกันด้วยวิธีต่างๆ เช่น อาจจะนำ output ของ layer ท้าย ๆ ป้อนกลับเข้าไปใน layer ก่อนหน้าพร้อมกับข้อมูลใหม่ (Recurrent Neural Network) หรืออาจจะเลือกที่จะเชื่อม layer ต่าง ๆ โดยเชื่อมเฉพาะ neuron ที่อยู่ใกล้กันเท่านั้น ไม่ได้เชื่อมหมดทั้ง layer (Convolutional Neural Network) เนื่องจากโมเดลในตระกูลนี้ที่สร้างจาก Perceptron สามารถเชื่อมต่อกันได้หลายแบบ จึงได้ถูกตั้งชื่อเรียกรวม ๆ กันว่า Artificial Neural Network นั่นเอง
การฝึกฝนโมเดล Artificial Neural Network
เริ่มจากเลือกฟังก์ชัน $L$ ที่ใช้เป็นตัวแทนความคลาดเคลื่อนของโมเดล (Loss function) โดยทั่วไปสำหรับปัญหาประเภททำนาย หรือพยากรณ์ค่าตัวเลข (Regression) มักจะเลือก mean squared error ซึ่งประเมิน จากความคลาดเคลื่อนของโมเดลที่พลาดไปจากข้อมูลจริง ส่วนปัญหาประเภทจำแนกแยกแยะประเภทข้อมูล (Classification) มักจะเลือก cross entropy loss ซึ่งประเมิน จากความน่าจะเป็นที่โมเดลคำนวณออกมาสำหรับข้อมูลในแต่ละประเภท เมื่อเลือกประเภทของ Loss function ได้แล้วจึงทำการฝึกฝนด้วยอัลกอริทึม gradient descent ดังต่อไปนี้
- สุ่มค่าน้ำหนักเริ่มต้น $\mathbf{w}$ และเลือกค่า learning rate $r$ ระหว่าง 0 กับ 1
- ทำซ้ำ
- คำนวณค่า gradient ของ $L$ คือ $\nabla L(\mathbf{w})$
- ปรับปรุงค่า $\mathbf{w} = \mathbf{w} – r\nabla L(\mathbf{w})$
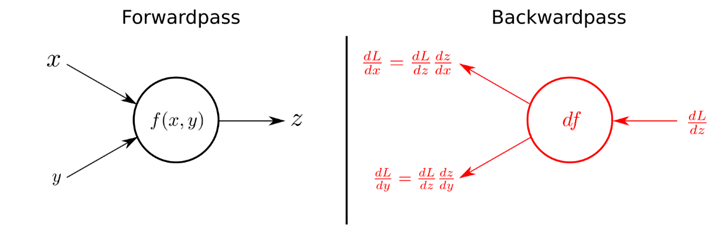
ค่า gradient ของ $L$ นั้นใช้เวลานานหากทำการคำนวณโดยตรง เนื่องจากค่า $L$ นั้นขึ้นกับค่า $\mathbf{w}$ ของทุกๆ layer ทำให้ต้องคำนวณค่า partial derivative จำนวนมาก ในทางปฏิบัติจึงใช้อัลกอริทึม backpropagation มาช่วยให้การคำนวณนี้เร็วขึ้น โดยเป็นการส่งค่า partial derivative ของ layer หลัง ๆ กลับไปให้ layer ก่อนหน้าเพื่อใช้ในการคำนวณ gradient ของ layer ก่อนหน้าได้ ซึ่งเป็นหลักการของการเขียนโปรแกรมแบบไดนามิค (Dynamic programming)
ข้อดีของ neural network
- เป็นโมเดลที่มีความยืดหยุ่นสูงมาก โดย neural network ที่มี 1 hidden layer ที่ไม่จำกัดขนาด สามารถใช้ในการประมาณค่าฟังก์ชันต่อเนื่องใด ๆ ก็ได้ (Universal approximation theorem)
- สามารถเรียนรู้ feature ต่าง ๆ ของข้อมูลได้ด้วยตนเองทำให้ลดความจำเป็นในการทำ feature engineering
ข้อเสียของ neural network
- มีจำนวนพารามิเตอร์ $\mathbf{w}$ และ $b$ ที่ต้องฝึกฝนจำนวนมาก ทำให้ใช้เวลาในการฝึกฝนนานกว่าโมเดลอื่น ๆ
- ต้องใช้ข้อมูลในการฝึกฝนจำนวนมากจึงจะได้ผลลัพธ์ที่น่าพอใจ หากข้อมูลที่ใช้ฝึกฝนน้อยเกินไปอาจจะมีประสิทธิภาพด้อยกว่าโมเดลอื่น ๆ ที่เรียบง่ายกว่าได้
- ไม่มีสูตรตายตัวในการเลือกวิธีเชื่อมต่อ layer ต่าง ๆ เลือกจำนวน layer และเลือกจำนวน neuron ในแต่ละ layer ทำให้ใช้เวลานานในการลองผิดลองถูกก่อนที่จะได้โมเดลคุณภาพสูง บ่อยครั้งที่โมเดลที่มีจำนวน layer น้อยกว่าอาจจะมีประสิทธิภาพสูงกว่าโมเดลที่มีจำนวน layer มากก็เป็นไปได้
ผู้เขียนหวังว่าผู้อ่านจะได้รับความเข้าใจถึงที่มา หลักการทำงานในทางเทคนิคของ neural network รวมถึงข้อดีข้อเสียของโมเดลชนิดนี้ และได้รับความรู้เพียงพอที่จะช่วยประกอบในการนำโมเดลไปใช้งานต่อ ว่าควรจะใช้โมเดลชนิดนี้หรือไม่ หรือควรจะใช้โมเดลชนิดอื่นที่มีความเรียบง่ายมากกว่านี้ สุดท้ายนี้ผู้อ่านสามารถทดลองสร้างโมเดล neural network ของตัวเองได้ที่เว็บไซต์ https://playground.tensorflow.org/ ขอให้สนุกกับการสร้างโมเดลนะครับ อีกสักนิดก่อนจากกัน ผู้เขียนอยากขอแนะนำบทความ AI กับการอ่านสัญญาณสมองมนุษย์ ซึ่งเกี่ยวกับระบบประสาทของมนุษย์จริง ๆ ไว้ให้เพิ่มเติมนะครับ
เอกสารอ้างอิง
- Perceptron – Wikipedia (https://en.wikipedia.org/wiki/Perceptron)
- Multilayer Perceptron – Wikipedia (https://en.wikipedia.org/wiki/Multilayer_perceptron)
- Concise Machine Learning (https://people.eecs.berkeley.edu/~jrs/papers/machlearn.pdf)
เนื้อหาโดย ไพโรจน์ เจริญศรี
ตรวจทานและปรับปรุงโดย เมธิยาภาวิ์ ศรีมนตรินนท์
