บทความที่แล้ว เราได้พาท่านผู้อ่านไปรู้จักกับ Survival Analysis ในเบื้องต้นว่าคืออะไร พร้อมกับกรณีตัวอย่างการประยุกต์ใช้ นอกจากนี้ผู้อ่านก็ได้ทำความรู้จักกับ Censored Data ประเภทต่าง ๆ กันมาแล้ว ถ้าใครยังไม่รู้จัก Survival Analysis กับ Censored Data แนะนำให้เข้าไปอ่านบทความแรกก่อนใน Survival Analysis กับความท้าทายในการจัดการ Censored Data Part 1 ส่วนในบทความนี้จะมาเล่าต่อถึง รายละเอียดของวิธีการในการวิเคราะห์ Survival Analysis กัน รวมถึง Term ต่าง ๆ ที่ควรรู้จัก และประเภทของวิธีการทาง Survival Analysis
Survival Analysis นั้นถูกพัฒนาขึ้นมาเพื่อจัดการปัญหา ของการเกิด Censored Data และถึงแม้ว่าข้อมูลของเราสามารถสังเกตหรือเก็บผลของการเกิดเหตุการณ์ได้ทุกตัวอย่าง คือทราบว่าเกิดเหตุการณ์ในช่วงเวลาเท่าไหร่ในทุกตัวอย่าง หรือ ไม่มีการเซ็นเซอร์เกิดขึ้นเลย วิธีการทาง Survival Analysis นี้ก็ยังเป็นเครื่องมือที่มีประโยชน์สำหรับการทำความเข้าใจ ระยะเวลาและอัตราของการเกิดเหตุการณ์ที่เราสนใจได้เช่นเดียวกัน
ในตัวอย่างจากบทความที่แล้ว จะเห็นว่าเราให้ทุกตัวอย่างมีจุดเริ่มต้นการเกิด ณ จุดเดียวกัน แต่ในความเป็นจริงจุดเริ่มต้นของแต่ละตัวอย่างอาจไม่จำเป็นต้องเริ่มต้นที่จุดเดียวกันก็ได้ ตัวอย่างเช่น สมมุติเราสนใจเกี่ยวกับช่วงเวลาการเป็นสมาชิกของลูกค้า จุดเริ่มต้นการเกิดของตัวอย่างนี้ ก็อาจจะเป็นวันที่ลูกค้ายืนยันการลงทะเบียนเข้าเป็นสมาชิก ซึ่งลูกค้าแต่ละคนสามารถเข้ามาสมัครเป็นสมาชิกในเวลาใดก็ได้ ดังนั้น ในการวิเคราะห์การรอดชีพ หรือ Survival Analysis จริง ๆ จะสนใจแค่ ช่วงเวลา (duration) ของการเกิดเหตุการณ์เท่านั้น ไม่จำเป็นต้องรู้เวลาจริงของจุดเริ่มต้นและจุดจบ
ก่อนอื่นขอพาท่านผู้อ่านไปรู้จักกับคำนิยามพื้นฐานและแนวคิดที่เกี่ยวข้องกับ Survival Analysis ได้แก่ Survival Function และ Hazard Function จากนั้นจะตามด้วยตัวอย่าง การประมาณค่าด้วยวิธีการ Kaplan-Meier
Survival Function
[latexpage] สมมุติให้ $T$ เป็นเวลาการรอดชีวิต หรือระยะปลอดเหตุการณ์ ของประชากรที่เราทำการศึกษา ซึ่งสามารถเป็นค่าเวลาไม่จำกัด (Infinite Time) ได้ หากไม่มีเหตุการณ์นั้นเกิดระหว่างช่วงเวลาการศึกษา Survival Function, $S(t)$, ของประชากรกลุ่มนี้จะถูกกำหนดด้วยสมการ
$S(t)$=ความน่าจะเป็นที่ยังไม่ตายที่เวลา ณ เวลา $t= P(T>t)$
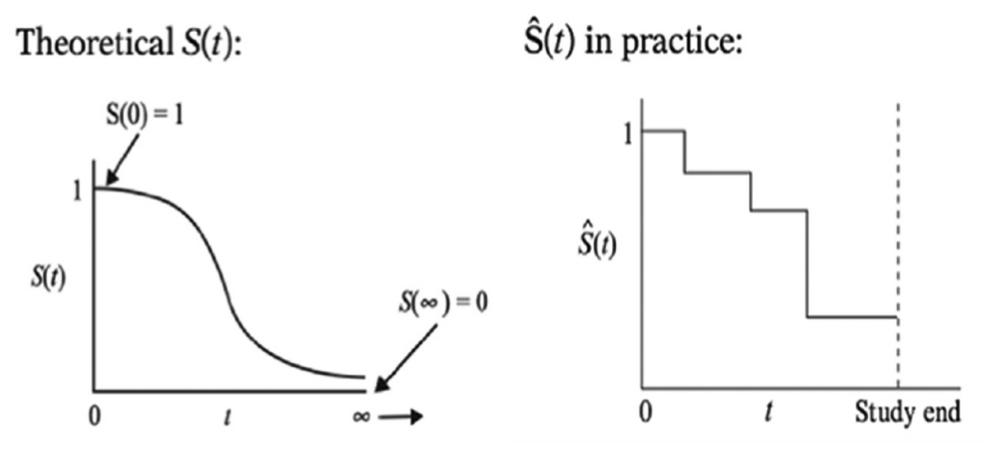
โดยเป็นฟังก์ชันที่บอกถึงความน่าจะเป็นที่ตัวอย่างหนึ่งยังคงปลอดเหตุการณ์ ณ เวลา $t$ หรือความน่าจะเป็นที่จะเกิดเหตุการณ์หลังจากเวลา $t$ ผ่านไปแล้ว หรือเรียกว่าเป็นค่า Survival Probability ที่มีการเปลี่ยนแปลงไปตามเวลา โดย Survival Function จะมีลักษณะดังรูปตัวอย่างด้านล่าง
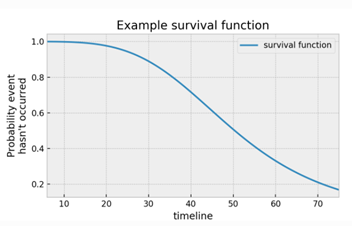
ยกตัวอย่างการตีความจากกราฟนี้ จะเห็นว่าที่ $S(40)$ มีค่าเท่ากับ 0.75 หมายถึงหลังจากผ่านไป 40 วัน นับตั้งแต่วันเริ่มต้นของการเกิดตัวอย่าง ความน่าจะเป็นที่ตัวอย่างจะอยู่รอด มีค่าเป็น 0.75 หรืออธิบายง่าย ๆ ได้ว่า 75% ของประชากรทั้งหมดจะอยู่รอด ณ วันที่ 40 ถ้าหากว่าตัวอย่างใดยังมีชีวิตจนจบช่วงเวลาการทดลอง ข้อมูลเหล่านั้นก็จะถูก Censored หรือก็คือไม่ทราบช่วงเวลาจริงของการตายของตัวอย่างนั้น ๆ นั่นเอง
โดย Survival Function จะมีคุณสมบัติหลัก ๆ ดังนี้
- $0 leq S(t) leq 1$ค่าความน่าจะเป็น มีค่าได้ตั้งแต่ 0-1
- $S(t)$ เป็นฟังก์ชันไม่เพิ่มตามเวลา โดยจะเริ่มต้นที่ 1 ที่ $t=0$ (100 % ของตัวอย่างในประชากรยังไม่มีการเกิดเหตุการณ์ขึ้น)
ณ จุดเริ่มต้นของการศึกษา $(t=0)$ ไม่มีตัวอย่างใดในกลุ่มประชากรที่ผ่านการประสบเหตุการณ์มาก่อน ดังนั้น ความน่าจะเป็นของการรอดชีวิตผ่านเวลา $t=0$ หรือ $S(0)$ จะมีค่าเป็น 1 หมายถึงประชากร 100% มีชีวิตอยู่รอดโดยปลอดเหตการณ์ เมื่อผ่านเวลา $t=0$ และหากว่าระยะเวลาของการศึกษาไม่มีจำกัด ก็คือทำการสังเกตไปได้เรื่อย ๆ จนกว่าตัวอย่างทั้งหมดจะเกิดเหตุการณ์ขึ้น โดยเราจะเชื่อว่าสักวันทุกตัวอย่างต้องประสบกับเหตุการณ์ จึงทำให้ความน่าจะเป็นจะค่อย ๆ ลดลงจนเหลือศูนย์ในที่สุด ในทางทฤษฎีนั้น Survival Functionจะเป็นกราฟที่มีลักษณะเป็นเส้นโค้งราบเรียบ แต่ในทางปฏิบัติแล้วการสังเกตผลลัพธ์ของการเกิดเหตุการณ์มักจะทำการสังเกตเป็นเวลาที่ไม่ต่อเนื่อง ส่วนมากจะอยู่ในหน่วย เช่น วัน หรือ เดือน ด้วยเหตุนี้เองกราฟของ Survival Function ในทางปฏิบัติจึงมีหน้าตาเป็น Step คล้ายขั้นบันได
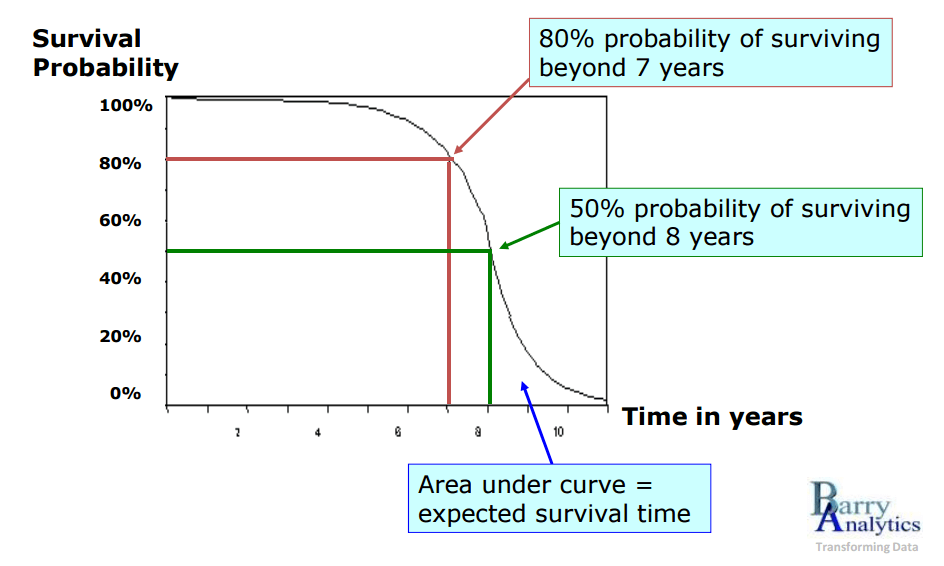
Survival Function นี้สามารถนำมาใช้ในการประมาณการค่าเวลา $T$ ของการรอดชีวิตได้ ตามเกณฑ์ความน่าจะเป็นที่เรากำหนด ยกตัวอย่างเช่น เรื่องการย้ายค้ายมือถือ บริษัทผู้ให้บริการเครือข่าย สามารถนำข้อมูลประวัติการย้ายค่ายของลูกค้าในอดีตมาสร้างเป็น Survival Function เพื่อใช้ในการประมาณระยะเวลาที่ลูกค้าจะย้ายค่าย สมมุติหากเราได้ Survival Function เป็นดังภาพตัวอย่างด้านล่าง แสดงให้เห็นว่าโอกาสที่ลูกค้าจะยังไม่ย้ายค่ายเกิน 50 % จะอยู่ในช่วง 8 ปีแรก ดังนั้น ถ้ากำหนดเกณฑ์ที่ความน่าจะเป็นเท่ากับ 50% จะให้มีการเสนอโปรโมชั่นให้แก่ลูกค้า เพื่อลดโอกาสที่ลูกค้าจะย้ายค่าย ถ้าปัจจุบันมีลูกค้าคนใดที่ใช้บริการกับบริษัทมาถึงปีที่ 8 ก็อาจจะมีการเริ่มให้พนักงานขายโทรไปหาลูกค้าเพื่อทำการเสนอโปรโมชั่นพิเศษ เป็นต้น
Hazard Function
จากนิยามของ Survival Function เราสนใจที่ความน่าจะเป็นของการรอดชีวิต หรือตัวอย่างที่ยังไม่เกิดเหตุการณ์ ณ เวลา $t$ ในทางกลับกันบางครั้งเราอยากสนใจอีกด้านคือ ความน่าจะเป็นของการเกิดเหตุการณ์ หรือการตายแทน เราจะใช้ฟังก์ชันที่ชื่อว่า Hazard Function, $h(t)$, โดย Hazard Function เป็นความเสี่ยงของการเกิดเหตุการณ์ใด ๆ ณ เวลาที่ $t$ โดยกำหนดให้ว่าไม่มีเหตุการณ์เกิดขึ้นมาก่อนเวลา $t$ นี้ หรืออธิบายง่าย ๆ ได้ว่า เป็นความน่าจะเป็นที่ถ้าคุณรอดชีวิต ณ เวลา $t$ แล้วคุณจะตายในจุดเวลาถัดไป โดยสามารถแทนด้วยสมการคณิตศาสตร์ได้ ดังนี้
$h(t) =$ ความน่าจะเป็นที่จะตาย ณ เวลา $t$
$$= lim_{ Delta t to 0} frac{P(t leq T < t + Delta t|T geq t )}{Delta t}$$
ยกตัวอย่างเช่น $h(200) = 0.7$ หมายถึงหลังจากผ่านไป 200 วัน หรือ ณ วันที่ 200 ความน่าจะเป็นของการตาย คือ 0.7 หรือ 70% โดยปกติแล้ว Hazard Rate จะเปลี่ยนแปลงตลอดเวลา โดยจะเริ่มต้น ณ เวลาใดก็ได้ และสามารถเป็นได้ทั้งขึ้นและลง
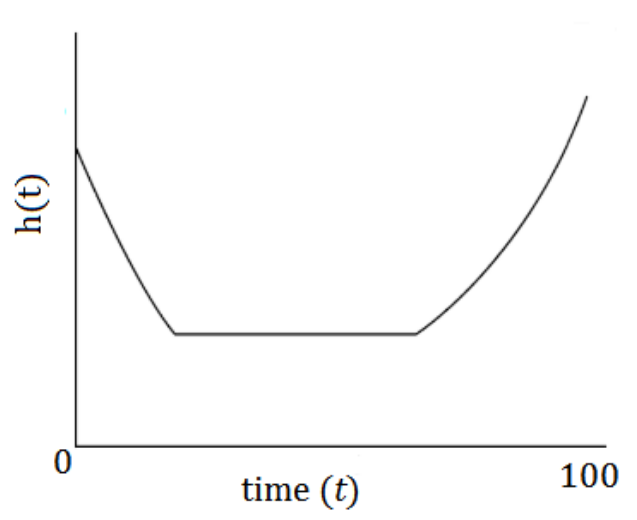
จากรูปด้านบนเป็นตัวอย่างในทางทฤษฎีของ Hazard Function กราฟรูปแบบนี้จะเรียกว่า bathtub curve ซึ่งจะมีหน้าตาคล้ายกับอ่างอาบน้ำตามชื่อ กราฟนี้แสดงความน่าจะเป็นของการเกิดเหตุการณ์ที่เราสนใจในแต่ละเวลาที่ผ่านไป กรณีตัวอย่างของการอธิบายกราฟนี้เช่น ความน่าจะเป็นของการยกเลิกการเป็นสมาชิกรับนิตยสารของลูกค้า จากกราฟอาจจะบอกได้ว่าในช่วง 30 วันแรก ความเสี่ยงที่ลูกค้าจะยกเลิกค่อนข้างสูงและลดลงมาเรื่อย ๆ จนถึงจุด ๆ หนึ่ง ความเสี่ยงก็จะเริ่มคงที่ จนกระทั่งความเสี่ยงค่อย ๆ เพิ่มขึ้นอีกครั้งเมื่อเวลาผ่าน ไประยะหนึ่ง เนื่องจากอาจจะเป็นเพราะลูกค้าเบื่อและต้องการเสพอะไรที่แปลกใหม่ เป็นต้น
Analysis of Survival Data
Survival Analysis สามารถถูกนำไปใช้ได้หลายรูปแบบ อาจจะแบ่งวิธีการต่าง ๆ ตามจุดประสงค์ได้ดังนี้
- เพื่ออธิบายระยะเวลาการอยู่รอด (Survival Time) ของสมาชิกในกลุ่ม เช่น
- Life tables
- Kaplan-Meier curve
- เพื่อเปรียบเทียบระยะเวลาการอยู่รอด (Survival Time) ระหว่างกลุ่มตั้งแต่ 2 กลุ่มขึ้นไป เช่น
- Log-rank test
- เพื่ออธิบายผลกระทบของปัจจัยต่าง ๆ ที่มีความสัมพันธ์ต่อระยะเวลาการอยู่รอด เช่น
- Cox proportional hazards regression
- Parametric Survival Models
- Survival Trees
- Survival Random Forest
Simple example of a Survival Curve by Kaplan-Meier Estimation
ถัดจากนี้ไป จะนำท่านผู้อ่านเข้าไปสู่การทำความเข้าใจกับตัวอย่างวิธีการคำนวณอย่างง่ายเพื่อสร้าง Survival Curve ขึ้นมา โดยตัวอย่างข้อมูลที่ยกมาในตารางด้านล่างนี้ เป็นชุดข้อมูลเล็ก ๆ ที่มีเพียง 5 ตัวอย่างข้อมูลเท่านั้น เพื่อให้เข้าใจวิธีการคำนวณแบบง่าย ๆ โดยชุดข้อมูลนี้ประกอบไปด้วย 2 คอลัมน์ ได้แก่ คอลัมน์ Survival Time ที่แสดงถึงช่วงเวลา และคอลัมน์ Event ที่แสดงถึงการเกิดขึ้นของเหตุการณ์ (1) หรือการเซ็นเซอร์ (0) โดยจะเป็นค่าที่บอกว่าช่วงเวลาในคอลัมน์ Survival Time นั้น หมายถึงช่วงเวลาของการเกิดเหตุกาณ์หรือช่วงเวลาจนถึงสิ้นสุดช่วงเวลาสังเกตและไม่สังเกตพบเหตุการณ์ใด ๆ ขึ้นจะเห็นได้ว่าในตัวอย่างนี้มีเพียงตัวอย่างเดียวเท่านั้นที่ถูกเซ็นเซอร์ นั่นก็คือหมายเลข 3 โดยเป็นตัวอย่างที่สังเกตไม่พบเหตุการณ์ และขาดการติดตามไป ตั้งแต่ เวลาที่ $t = 21$
| Subject | Survival Time (T) | Event (E) |
| 1 | 6 | 1 |
| 2 | 44 | 1 |
| 3 | 21 | 0 |
| 4 | 14 | 1 |
| 5 | 62 | 1 |
หนึ่งในวิธีการที่ง่ายที่สุดในการประมาณ Survival Function ก็คือการใช้วิธีประมาณด้วยวิธีการ Kaplan-Meier โดยสามารถทำการคำนวณหาค่าความน่าจะเป็น ณ เวลาต่าง ๆ ได้ด้วยสมการด้านล่างนี้
$$hat{S}(t) = prod_{t_i < t} left(1-frac{d_i}{n_i}right) = prod_{t_i < t} left(frac{n_i-d_i}{n_i}right) $$
โดย
- $d_i$ คือ จำนวนเหตุการณ์ตาย ณ เวลา $t$
- $n_i$ คือ จำนวนตัวอย่างที่มีความเสี่ยงที่จะตาย ณ ก่อนถึงเวลา $t$
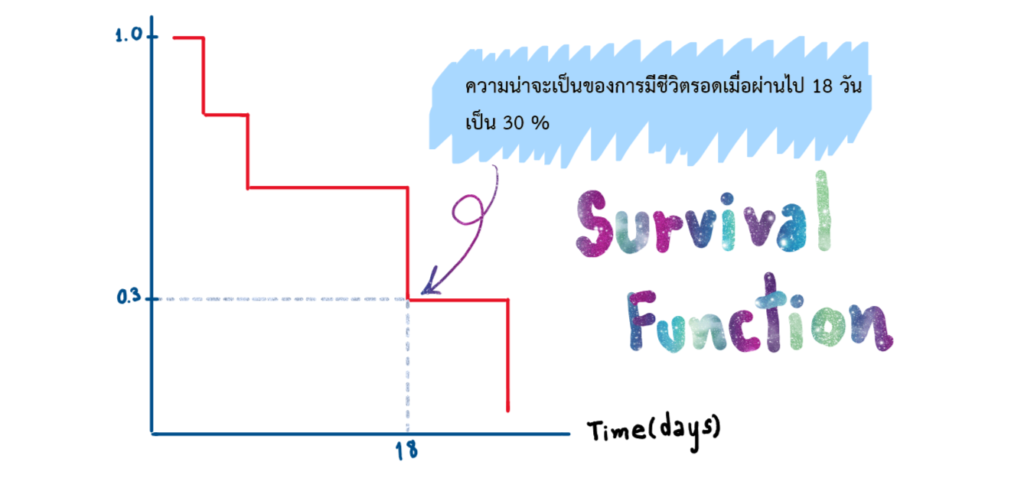
ซึ่งจากข้อมูลตัวอย่างเราจะสามารถ คำนวณค่า $S(t)$ ได้ ดังตารางด้านล่าง และเมื่อนำ $S(t)$ ที่คำนวณได้มาพล็อตก็จะได้ผลเป็นกราฟดังรูปด้านล่างนั่นเอง
| t | Calculation | S(t) |
| $0 leq t < 6$ | $frac{5-0}{5}$ | 1.0 |
| $6 leq t < 14$ | $1.0 times frac{5-0}{5}$ | 0.8 |
| $14 leq t < 21$ | $1.0 times frac{4}{5} times frac{4-1}{4}$ | 0.6 |
| $21 leq t < 44$ | $1.0 times frac{4}{5} times frac{3}{4} times frac{3-0}{3}$ | 0.6 |
| $44 leq t < 62$ | $1.0 times frac{4}{5} times frac{3}{4} times frac{3}{3} times frac{3-1}{3}$ | 0.3 |
| $t leq 62$ | $1.0 times frac{4}{5} times frac{3}{4} times frac{3}{3} times frac{2}{3} times frac{2-1}{2}$ | 0 |
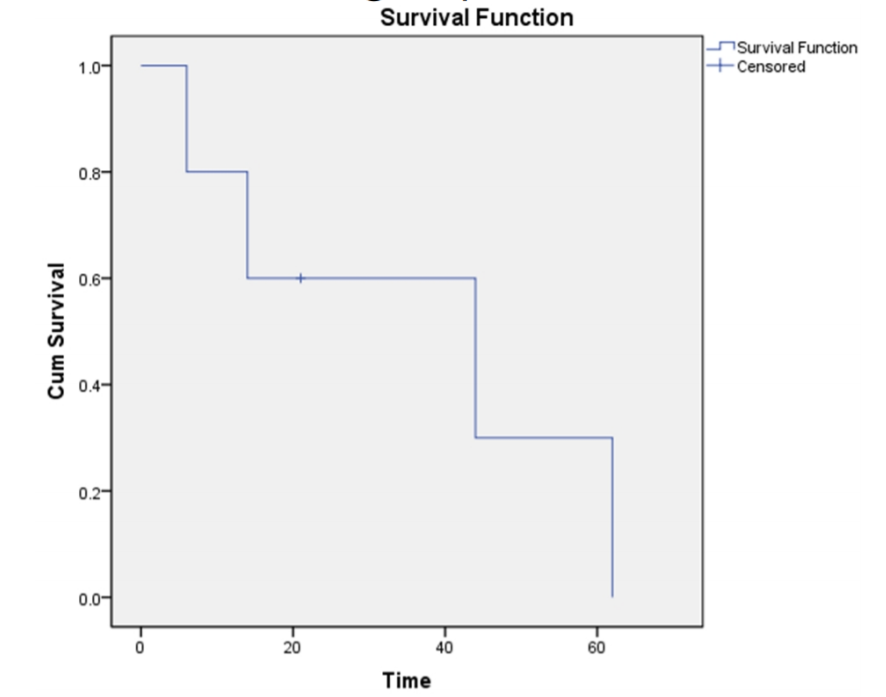
และนี่ก็คือตัวอย่างหนึ่งของการทำ Survival Analysis โดยเป็นการคำนวณ Survival Function แบบง่าย ด้วยวิธีการที่มีชื่อว่า Kaplan-Meier ซึ่งจะใช้ในการวิเคราะห์ภาพรวมของประชากรทั้งหมดของกลุ่ม ว่ามีอัตราการรอดชีวิต หรือความเสี่ยงในแต่ละช่วงเวลาเปลี่ยนแปลงไปอย่างไร นอกจากนี้ศาสตร์ของ Survival Analysis ยังมีวิธีการอื่น ๆ ที่ถูกนำมาใช้เพื่อการวิเคราะห์ในวัตถุประสงค์ที่แตกต่างกันอีกหลายวิธี เช่น การวิเคราะห์ปัจจัยของประชากร 2 กลุ่ม ที่ส่งผลต่อระยะเวลาการมีชีวิตที่แตกต่างกัน ก็จะมีวิธีการที่เรียกว่า Cox proportional hazards regression เป็นต้น ซึ่งก็อาจจะมีโอกาสได้มาเล่าให้ฟังต่อในบทความถัด ๆ ไป
ที่มา:
https://medium.com/analytics-vidhya/survival-analysis-using-lifelines-in-python-bf5eb0435dec
https://humboldt-wi.github.io/blog/research/information_systems_1920/group2_survivalanalysis/
http://classroom.takasila.org/classroom/dataupload/takasila/155/SurvivalAnalysis_SC56.pdf
https://altis.com.au/a-crash-course-in-survival-analysis-customer-churn-part-i/
Project Manager & Data Scientist
Big Data Institute (Public Organization), BDI
- Kanyawee Pornsawangdeehttps://temp.bdi.or.th/en/author/kanyawee-po/
- Kanyawee Pornsawangdeehttps://temp.bdi.or.th/en/author/kanyawee-po/
- Kanyawee Pornsawangdeehttps://temp.bdi.or.th/en/author/kanyawee-po/31 August 2022
- Kanyawee Pornsawangdeehttps://temp.bdi.or.th/en/author/kanyawee-po/